Podemos relacionar à Geometria plana os seguintes conteúdos programáticos:
Posições relativas entre retas
Ângulos
Triângulos
Quadriláteros
Polígonos
Perímetro
Áreas de regiões planas
ÂNGULOS
Denominamos por ângulo a abertura formada por duas semirretas que possuem a mesma origem.
A unidade usual de ângulo é o grau (representado por º), por exemplo:
25º: lê-se vinte e cinco graus.
32º: lê-se trinta e dois graus.
120º: lê-se cento e vinte graus.
O grau possui dois submúltiplos: o minuto (representado por ’) e o segundo (representado por ”). Observe: 32’: lê-se trinta e dois minutos.
81’: lê-se oitenta e um minutos.
15”: lê-se quinze segundos.
45”: lê-se quarenta e cinco segundos.
transformações a seguir:
2º em minutos: 2 * 60 = 120’
12’ em segundos: 12 * 60 = 720”
3600’’ em minutos: 3600 : 60 = 60’
90000” em graus: 90000 : 60 = 1500’ e 1500 : 60 = 25º
O objeto capaz de medir o valor de um ângulo é chamado de transferidor, podendo ele ser de “meia volta” (180º) ou volta inteira (360º).
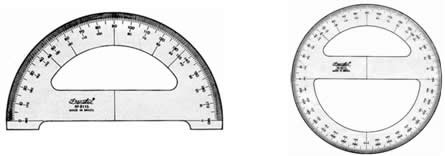
Tabela de conversões:
Adição
Dado os ângulos de 6º 25’ 36” e 4º 40’ 30”, a soma entre eles é:
O resultado da soma é 10º 65’ 66”, porém podemos apresentar o resultado de uma outra forma. Acompanhe a demonstração:
No ângulo de medida 10º 65’ 66”, temos que 65’ = 60’ + 5’ = 1º + 5’ e 66” = 60” + 6” = 1’ + 6”. Dessa forma, 10º 65’ 66” = 11º 6’ 6”.
Subtração
Dados os ângulos 54º 16’ 32” e 27º 18’ 40”, a subtração entre eles é:
Observe que existem valores no minuendo que são menores dos que os valores do subtraendo, quando isso acontece na subtração temos que tirar do valor da esquerda completando o que está menor.
Ao retirarmos 1’ de 16’ ficaremos com 15’, sendo que 1’ = 60” o qual deve ser somado a 32” resultando em 92”.
Agora devemos retirar 1º de 54º que será igual à 53º, considerando que 1º = 60’, temos 60’ + 15’ = 75’. Portanto:
O resultado da subtração é igual a 26º 57’ 52”.
Classificação de ângulos
Os ângulos são classificados de acordo com suas medidas:
Agudo: ângulo com medida menor que 90º.
Reto: ângulo com medida igual a 90º.
Obtuso: ângulo com medida maior que 90º.
Raso: ângulo com medida igual a 0º ou 180º.
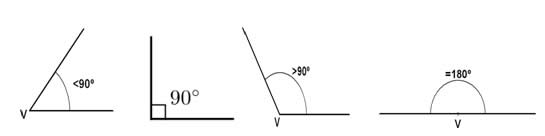
agudo reto obtuso raso
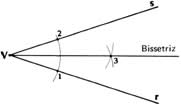
Bissetriz de um ângulo
Bissetriz de um ângulo pode ser definida como a semirreta que se origina no vértice do ângulo principal, dividindo-o em outros dois ângulos com medidas iguais.
Retas paralelas cortadas por uma transversal
Ângulos correspondentes: a e e, d e h, b e f, c e g Congruentes
Ângulos colaterais externos: a e h, b e g Suplementares
Ângulos colaterais internos: e e d, c e f Suplementares
Ângulos alternos externos: a e g, b e h Congruentes
Ângulos alternos internos: d e f, c e e Congruentes
ESPERO QUE EU TENHA ESCLARECIDO ALGUMAS DÚVIDAS, LEMBRE-SE QUE AQUI VCS TERÃO APENAS UMA AJUDA, APROFUNDEM LENDO NOS OUTROS SITES, LIVROS E FAZENDO OS EXERCÍCIOS, ASSIM VCS OBTERÃO O SUCESSO NECESSÁRIO PARA AS APROVAÇÕES NOS CONCURSOS E VESTIBULARES DA VIDA ...ABRAÇO A TODOS!!!
