HISTÓRIA DA EQUAÇÃO DO 2º GRAU E SUAS RESOLUÇÕES

As equações do segundo grau são abordadas na história da matemática desde a época dos egípcios, babilônios, gregos, hindus e chineses.

O primeiro registro das equações polinomiais do 2.o grau foi feita pelos babilônios. Eles tinham uma álgebra bem desenvolvida e resolviam equações de segundo grau por métodos semelhantes aos atuais ou pelo método de completar quadrados. Como as resoluções dos problemas eram interpretados geometricamente não fazia sentido falar em raízes negativas. O estudo de raízes negativas foi feito a partir do século XVIII. Como eles não utilizavam coeficientes negativos, precisavam distinguir diferentes casos possíveis: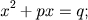

• 
• 
•  
•  
•  
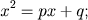
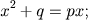
• O Caso 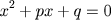com p e q positivos obviamente não teria solução. Na Grécia, a matemática tinha um cunho filosófico e pouco prático. Euclides, nos Elementos resolve equações polinomiais do 2.o grau através de métodos geométricos. Diophanto contribuiu para mais um avanço na busca da resolução de equações do 2.o grau ao apresentar uma outra representação da equação introduzindo alguns símbolos, pois até então a equação e sua solução eram representados em forma discursiva. Na Índia as equações polinomiais do 2.o grau era resolvidas completando quadrados. Esta forma de resolução foi apresentada geometricamente por Al-Khowârizmî, no século IX. Eles descartavam as raízes negativas, por serem "inadequadas" e aceitavam as raízes irracionais. Tinham também uma "receita" para a solução das equações de forma puramente algébrica. A abordagem chinesa para a resolução destas equações foi o método fan-fan, publicado por Zhu Shijie (também chamado de Chu Shih-Chieh), no século XIII, no seu Tratado das Nove Seções. O método foi redescoberto no século XIX, pelos ingleses William George Horner e Theophilus Holdred e, um pouco antes, pelo algebrista italiano Paolo Ruffini . O método fan-fan ficou conhecido na Europa como método de Horner. Na verdade, ele já tinha sido antecipado por Isaac Newton em 1669. No século XVI, François Viéte utilizou-se de simbolismo para representar equações dando um carater geral. Bhaskara à fórmula que dá as soluções da equação do segundo grau. Além de ser historicamente incorreto, esta nomenclatura não é usada em nenhum outro país (veja a respeito a Revista do Professor de Matemática, 39(1999), p. 54).  

OBSERVAÇÃO: No Brasil, costuma-se chamar de fórmula de Bhaskara à fórmula que dá as soluções da equação do segundo grau. Além de ser historicamente incorreto, esta nomenclatura não é usada em nenhum outro país (veja a respeito a Revista do Professor de Matemática, 39(1999), p. 54).

O Teorema de Tales e sua história

Há duas versões para este fato. Hicrônimos, discípulo de Aristóteles, diz que Tales mediu o comprimento da sombra da pirâmide no momento em que nossas sombras são iguais a nossa altura, assim medindo a altura da pirâmide. A de Plutarco diz que fincando uma vara vertical no extremo da sombra projetada pela pirâmide, construímos à sombra projetada da vara, formando no solo dois triângulos semelhantes.

Notamos que neste relato é necessário o conhecimento de teoremas sobre triângulos semelhantes. Observando o desenho abaixo, a vara colocada no extremo C da sombra da pirâmide forma, com sua sombra, o triângulo DCE que é semelhante ao triângulo ABC. 

Medindo as duas sombras e a altura da vara, pode-se determinar então a altura da pirâmide. 

 

                           Para alguns historiadores da matemática antiga, a geometria demonstrativa iniciou-se com Tales de Mileto, um dos sete sábios da Grécia. Foi o fundador da escola jônica, escola de pensamento dedicada à investigação da origem do universo e de outras questões filosóficas, entre elas a natureza e a validade das propriedades matemáticas dos números e das figuras. 

Tales é uma figura imprecisa historicamente, pois não sobreviveu nenhuma obra sua. O que sabemos é baseado em antigas referências gregas à história da matemática que atribuem à ele um bom número de descobertas matemáticas definidas. Pouco sabemos sobre a vida e obra de Tales. Supõe-se que começou sua vida como mercador, tornando-se rico o suficiente para dedicar a parte final de sua vida ao estudo e a realização de algumas viagens. Supõe-se que viveu algum tempo no Egito onde provavelmente aprendeu geometria e na Babilônia onde entrou em contato com tabelas e instrumentos astronômicos. Faz parte do seu mito o fato de ter previsto o eclipse solar de 585 a.C., embora muitos historiadores da ciência duvidem que os meios existentes na época permitissem tal proeza. Atribui-se a Tales o cálculo da altura das pirâmides, bem como o cálculo da distância até navios no mar, por triangulação. Tales foi o primeiro personagem conhecido a quem associam-se descobertas matemáticas. Acredita-se que obteve seus resultados mediante alguns raciocínios lógicos e não apenas por intuição ou experimentação. Os fatos geométricos cuja descoberta é atribuída a Tales são:

• A demonstração de que os ângulos da base de dois triângulos isósceles são iguais;
• A demonstração do seguinte teorema: se dois triângulos tem dois ângulos e um lado respectivamente iguais, então são iguais;
• A demonstração de que todo diâmetro divide um círculo em duas partes iguais;
• A demonstração de que ao unir-se qualquer ponto de uma circunferência aos extremos de um diâmetro AB obtém-se um triângulo retângulo em C. Provavelmente, para demonstrar este teorema, Tales usou também o fato de que a soma dos ângulos de um triângulo é igual a dois retos;
• Tales chamou a atenção de seus conterrâneos para o fato de que se duas retas se cortam, então os ângulos opostos pelo vértice são iguais. 
 

 Neste modelo podemos observar claramente os segmentos proporcionais proposto por Tales

Aqui percebemos que todo triângulo pode ser decomposo em segmentos proporcionais.