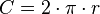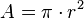Resolução das questões do aulão meta

View more documents from Gledson Guimarães.

pessoal aí estão quatro questões resolvidas das que escolhi para debater no aulão de hoje no META

3º aulão meta ...QUESTÕES E RESOLUÇÕES

View more presentations from Gledson Guimarães.
 

3º AULÃO META PARA O ENEM!

FOI UM SUCESSO O AULÃO, MUITO LEGAL GENTE, HOJE DIA 30/10/10 OS ALUNOS DO META, MOSTRARAM QUE ESTÃO QUERENDO TIRAR A MAIOR NOTA POSSÍVEL NO ENEM QUE SERÁ REALIZADO PRÓXIMO FIM DE SEMANA... SUCESSO MEUS QUERIDOS ACREDITO MUITO EM VOCÊS E NO TRABALHO QUE DESENVOLVEMOS AO LONGO DESSE ANO. O RESUMO DO AULÃO DE HOJE ESTÁ AÍ...

 Nossos alunos META assistiram aulas de  português, história, inglês, espanhol, geografia, filosofia, biologia, física, química e matemática

I aulão META

View more presentations from Gledson Guimarães.

Esse foi o primeiro aulão realizado pelo Meta em Santa Cruz do Capibaribe _ PE...foi muito legal, uma grande aceitação por parte dos alunos...espero que vcs possam aproveitar cada vez mais o espaço para tirarem dúvidas...pode  enviar nos comentários as dúvidas pois terei um enorme prazer em respondê-las... e não esqueçam que domingo estarei postando o resumão do aulão de sábado para o ENEM...

GALERA, AQUELE ABRAÇO! ESTUDEM POIS O SUCESSO É CERTO...

undefined

Geometria analítica retas exercicios by gledson

View more presentations from Gledson Guimarães.

ESTUDAR AS RETAS NO PLANO CARTESIANO É FUNDAMENTAL PARA A GALERA QUE VAI PRESTAR VESTIBULAR NA ÁREA DE EXATAS...E SEMPRE REPITO: RETAS, CIRCUNFERÊNCIAS E CÔNICAS SÃO A "TRINDADE" EM MATEMÁTICA  NA PARTE DE ANALÍTICA... SEMPRE ESTEJAM ATENTOS AS EQUAÇÕES DE UMA RETA, QUE PODE SER: GERAL, REDUZIDA, SEGMENTÁRIA E  PARAMÉTRICA , ESSAS SÃO AS PRINCIPAIS E AS SUFICIENTES PARA RESOLVEREM OS PROBLEMAS NO QUE TANGE  A GEOMETRIA ANALÍTICA

Funçoes, graficos by gledsonOBSERVEM AS SEMELHANÇAS E DIFERENÇAS QUE EXISTEM ENTRE UM TIPO DE FUNÇÃO E OUTRA..QUAIS AS CARACTERÍSTICAS ENTRE OS DIFERENTES TIPOS DE GRÁFICOS DE FUNÇÕES, SUAS  INVERSAS E COMO PODEREMOS DEDUZIR PROPRIEDADES ATRAVÉS DE GENERALIZAÇÕES....

View more presentations from Gledson Guimarães.

NUNCA ESQUEÇA QUE FUNÇÕES SÃO RELAÇÕES MATEMÁTICAS QUE OBEDECEM AO PRINCÍPIO DA CORRESPONDÊNCIA BIUNÍVOCA

 

Geometria espacial BY GLEDSON

View more presentations from Gledson Guimarães

Mais do que saber nomes de prismas e pirâmides, é saber para que eles servem em nossa vida cotidiana... ao estudarem Geometria estejam atentos às propriedades fundamentais de cada sólido, aos Teoremas envolvidos na Geometria Plana, que é fundamental, para um bom conceito desenvolvido na Espacial.

Estejam atentos às generalizações que sempre fazemos ao final de cada estudo de sólido geométrico e os principais conteúdos explorados para concursos, diz respeito aos cenceitos de áreas e volumes..Bons estudos pessoal...abração 

Funções trigonometricas BY GLEDSON

View more presentations from Gledson Guimarães.
NÃO TENHAM MEDO DA TRIGONOMETRIA, ELA NÃO MORDE! PORÉM COSTUMA DEIXAR  A GALERA NA MÃO NOS VESTIBULARES...DECORAR NÃO É O CAMINHO POIS EXISTEM SITUAÇÕES ONDE RESOLVER SITUAÇÕES TRIGONOMETRICAS NÃO DEPENDEM APENAS DE UMA FÓRMULA, OU TABELA E SIM DE UMA BOA INTERPRETAÇÃO DA SITUAÇÃO-PROBLEMA

GEOMETRIA ESPACIAL DE POSIÇÃO

View more presentations from Gledson Guimarães.

aqui teremos mais as teorias e teoremas que envolvem os conceitos básicos de reta, ponto e planos no espaço...muito fácil de compreender e não precisamos decorar nada, pois assimilamos sem perceber...

LOGARITMOS BY GLEDSON

View more presentations from Gledson Guimarães.

o pessoal reclama muito de logaritmos, mas sei porque...afinal é necessário dominar  bem exponenciais, potenciação e radicais para  uma boa e eficiente aprendizagem...metam a cara nos estudos!!!

Função exponencial

View more presentations from Gledson Guimarães.

para aprender bem exponencial é necessário saber bem potenciação e propriedades...tem muita gente que não consegue aprender bem exponenciais, por não saber potenciação.

ALGUMAS COISAS SOBRE O NOVO ENEM

Todo mundo anda preocupado com o novo ENEM.

Com 180 questões e dois dias de prova, a tendência  é que a dificuldade aumente consideravelmente. Dito isso, é importante que você tenha em mente os conteúdos necessários para estudar.

O que estudar para a prova de Matemática do ENEM?

• Aritmética em N
• Conjunto dos Números Racionais
• Conjunto dos Números Reais
• Unidades de Medida
• Cálculo Algébrico
• Matemática Comercial
• Função
• Função do 1º grau
• Função do 2º grau
• Função Modular

Geometria Plana

• Ângulo
• Polígonos
• Triângulo
• Quadriláteros
• Circunferência e Círculo
• Teorema de Thales
• Semelhança de Triângulos
• Relações Métricas no Triângulo Retângulo
• Relações Métricas num Triângulo Qualquer
• Relações Métricas na Circunferência
• Área das Figuras Planas

• Função Exponencial
• Logaritmo
• Polinômios
• Análise Combinatória
• Binômio de Newton
• Matriz
• Determinante
• Sistemas Lineares
• Progressão Aritmética e Progressão Geométrica

Geometria Espacial

• Prisma
• Pirâmide
• Cilindro
• Cone
• Esfera

Trigonometria

• Números Complexos
• Equações Algébricas

• Estudo Analítico da Reta
• Estudo Analítico da Circunferência
• Limite
• Derivada

  Algo que deve ser observado é que estes últimos conteúdos (limites e derivadas) não são estudados no Ensino Médio em  algumas regiões do Brasil, pois não são conteúdos tão primordiais ao ensino médio, já que esses são estudados no ensino superior. Vale a pena lembrar que todos os conteúdos são muitos importantes, mas existem competências importantíssimas em Matemática, como a leitura e interpretação de tabelas e gráficos, pois são elementos cada vez mais presentes em nosso dia a dia. Estejam atentos a isso.

 

Lembre-se de algo importante que todo concurseiro sabe: não deveremos perder tempo em questões que parassem ser duvidosas ou mesmo que não conseguimos entende-las. Após 5 minutos , se não sair nada na resolução, passe para questão posterior, pois em concursos o tempo deve ser utilizado de forma precisa!

O dia da prova

O tão esperado dia (dias) de prova chegou!! O nervosismo bate, dor-de-cabeça, mãos suando, branco….
Calma!

Essa é a palavra chave. Não pense nos concorrentes ao lado, e não ache que eles estão mais preparados do que você, tenha confiança! A dica é pensar que o dia da prova, é apenas mais um dia comum, mais um “simulado”, como vários que você deve ter feito antes.

Aqui vão algumas dicas para o DIA DA PROVA:

1. Relógio: tenha um bom relógio, de fácil visualização, e confira se a bateria está boa.

2. Roupas: use roupas leves e muito confortáveis, lembre-se de que você vai ficar sentado por várias horas! Leve também um casaquinho, se o tempo estiver instável. Frio ou calor pode tirar a concentração do candidato.

3. Água: essencial! Leve uma garrafinha de água e coloque na sua mesa. Ajuda a hidratar e relaxar. Mas não exagere na quantidade de água, pois pode dar vontade de ir ao toalete mais de uma vez (e aí perde-se tempo!)

4. Comece por questões mais trabalhosas: A cabeça no início da prova está mais descansada e isso facilita na resolução de questões mais difíceis. Escolha português (principalmente as de interpretação de texto) e de cálculos.

5. Comida: é bom levar algo para comer, mas dê preferencia à alimentos leves e energéticos, como chocolate, barra de cereais, frutas etc. Fuja de comidas “barulhentas” como os salgadinhos, vai tirar a sua concentração e dos outros candidatos.

6. Redação: é melhor fazê-la por último, quando toda a prova (ou quase toda) estiver resolvida. Eu (Gledson), prefiro fazer primeiro a Redação pois terei mais inspiração no início, do que no final da prova.

7. Tempo por matéria: o ideal é reservar um tempo médio para cada matéria, esse tempo pode variar de acordo com o grau de dificuldade das questões, quantidade de texto/cálculos, complexidade etc. É importante já ter feito alguns simulados antes para saber qual é o seu tempo médio por matéria, pois no dia da prova você pode estar mais nervoso e ter um tempo de referência.

E o mais importante: não se preocupe com os outros candidatos! Se a escola onde você foi fazer a prova estiver lotada, isso não quer dizer nada. Todos tem chance de passar, quem realmente estudou e se dedicou já tem meio caminho andado. 

 Muita atenção nos enunciados das questões !!!

Desde a alteração no formato do Enem, em 2009, é cobrado dos alunos maior aprofundamento nos conteúdos das disciplinas do Ensino Médio. Isso não elimina, contudo, a necessidade que os estudantes possuem em apresentar uma série de competências básicas, entre elas a de leitura e compreensão comunicativa.

Essa competência não está relacionada apenas à capacidade de ler e entender de textos, mas também de assimilar outras formas de comunicação (gráficos, imagens, mapas, tabelas). Assim, observando as provas anteriores, é possível perceber que, muitas vezes, a resposta das perguntas está contida no seu próprio enunciado.

Mesmo em questões sobre assuntos desconhecidos pelo aluno, a compreensão do enunciado pode trazer a resposta sem que o conteúdo específico seja dominado. Para a resolução desse tipo de questão, portanto, é necessária uma leitura atenta de seu enunciado, concentração e calma para assimilar as informações.

SIMULADOS PARA O ENEM

PRA VOCÊS QUE ESTÃO ESTUDANDO  MUITO PARA O ENEM E VESTIBULARES UMAS DICAS DE SITES QUE VOCÊS IRÃO ENCONTRAR VÁRIOS SIMULADOS...APROVEITEM BASTANTE...QUALQUER COISA PODEM ME ENVIAR DÚVIDAS QUE NA MEDIDA DO POSSÍVEL IREI SOLUCIONAR...ABRAÇOS 

VEJAM ALGUNS SITES

http://www.estudantes.com.br/simulado/sim_9_14.asp

http://noticias.terra.com.br/educacao/interna/0,,OI3861171-EI14112,00-Matematica.html

http://simuladonovoenem2010.com.br/resultado/index.asp

http://www.profcardy.com/exercicios/especial.php?facul=ENEM

http://www.enem.coc.com.br/simulado01.asp

ESSE  FIM DE MÊS É TEMPO DE REVER A MATÉRIA ESTUDADA, HÁ QUEM DIGA QUE ESTUDAR TUDO QUE FALTA AGORA AJUDA A LEMBRAR MAIS, PARTICULARMENTE NÃO ACREDITO TANTO...PRINCIPALMENTE EM MATEMÁTICA, QUE NÃO ADIANTA RESOLVER MUITOS PROBLEMAS E SIM POUCOS PROBLEMAS QUE VOCÊ SEJA CAPAZ DE ENTENDER E ASSIMILAR A TEORIA ENVOLVIDA NESSE PROBLEMA...

Desafios matemáticos valendo sete milhões de dólares 

O Clay Mathematics Institute,
sediado em Boston, organizou o Millenium Meeting que ocorreu, em maio de 2 000, na cidade de Paris. O objetivo desse encontro era celebrar a entrada do novo milênio, anunciando prêmios para a resolução de alguns problemas que tem grande chance de nortearem o desenvolvimento da Matemática no século XXI.

Foram selecionados sete problemas, a cada um sendo dotado um premio de um milhão de dólares pela resolução, de acordo com regras minuciosamente descritas e que podem ser consultadas no site da American Mathematical Society.

Esses problemas são bem conhecidos da comunidade matemática. Por ordem de antiguidade:

1. Resolução das equações de Navier-Stokes ( c. 1830 )
2. Hipótese de Riemann ( 1859 )
3. Conjectura de Poincaré ( 1904 )
4. Conjectura de Hodge ( 1950)
5. Resolução das equações de Yang-Mills ( 1950 )
6. Conjectura de Birch e Swinnerton-Dyer ( 1965 )
7. Problema P versus NP ( 1971 )

Como seria de se esperar, vários desses problemas são de formulação bem técnica, em muito ultrapassando os conhecimentos de Matemática Elementar, o tema deste site.

Contudo, temos algumas exceções como é o caso de um dos mais antigos desses problemas: a Conjectura de Poincaré.
De um modo simplificado, ela afirma que todo objeto limitado, sem "buracos" e com fronteira lisa pode ser deformado continuamente numa esfera. É fácil verificarmos isso para o caso de objetos concretos do espaço euclidiano tri-dimensional, como caixas e cilindros fechados ( um exemplo de objeto NAO incluído na conjectura é uma xícara; com efeito é fácil vermos que o buraco envolvido pela alça NAO desaparece com deformações contínuas da xícara; vendo de outro modo: SE a xícara não tivesse alça seria fácil deformá-la até uma esfera ).
A prova rigorosa - para o caso de três dimensões - foi dada próprio Poincaré. Contudo, mesmo depois de quase cem anos de esforços, ainda não se conseguiu fazer o mesmo para o caso de objetos do espaço euclidiano a quatro dimensões.

Outro aspecto interessante da lista é que inclui tanto problemas que parecem não ter nenhuma aplicabilidade, fora da Matemática, como problemas de imensa importância tecnológica. Por exemplo, o Problema "P versus NP" é de enorme relevância em campos que vão desde a Engenharia até a criptografia aplicada aos serviços militares e às transações comerciais e financeiras via Internet.

Esse problema, incidentalmente, é um outro que tem uma formulação fácil de ser entendida. De modo simplificado, ele pergunta se existem problemas matemáticos cuja resposta pode ser verificada em tempo prático ( por exemplo, em tempo polinomial ) MAS que não podem ser resolvidos ( diretamente, sem se ter um candidato à solução ) em tempo prático. Ilustrando: se alguém lhe disser que o número 13 717 421 pode ser escrito como o produto de dois outros inteiros, V. provavelmente demorará para provar isso; contudo, se lhe assoprarem que ele é o produto de 3 607 por 3 803, V. seria capaz de muito rapidamente verificar tal fato.

O problema "P versus NP" parte da constatação que são muito frequentes as situações em que parece ser muito mais rápido verificar solução do que achar um processo de resolução, e então pergunta: isso sempre ocorre, ou simplesmente ainda não descobrimos um modo de resolvê-los rapidamente?

Para uma discussão mais desenvolvida, mas ainda evitando tecnicalidades, sobre o Problema "P versus NP", V. pode visitar nossa página sobre o um outro problema clássico: O Problema do Caixeiro Viajante.

Quantas dimensões a física conhece?

por Victor Bianchin; Marina Motomura

Oficialmente, apenas quatro, mas há teorias que sugerem até dez dimensões. Uma das correntes científicas que defendem as dez dimensões é a Teoria das Supercordas, que afirma que as dez dimensões interagiriam entre si como as cordas de um violino. Mas tudo fica só na especulação: os próprios cientistas admitem que, com a tecnologia - atual, ainda não é possível comprovar as dez dimensões.


Os dez mandamentos
Na Teoria das Supercordas, dimensões vão de uma simples reta até um conjunto de big-bangs

1. Antes da primeira dimensão, existe a dimensão zero, que é apenas um ponto. A conexão entre dois pontos forma a primeira dimensão, que é uma reta. Nosso conceito de largura vem dessa conexão entre os pontos

2. O plano é a segunda dimensão. Para ser bidimensional, um objeto precisa de dois valores numéricos (correspondentes aos nossos conceitos de largura e comprimento) para ser situado, porque ele tem dois eixos

3. A terceira dimensão é o espaço. Para um objeto, isso significa ganhar profundidade e se tornar tridimensional, ou seja, ser dono de três valores numéricos que o situem (largura, comprimento e profundidade)

4. A quarta dimensão é a duração ou o tempo. Ela é a linha que leva cada ser quadrimensional (como nós, seres humanos) do começo (eu bebê) ao final da existência (eu velhinho). Nós não percebemos essa dimensão, por isso não podemos voltar ou avançar no tempo para ver nossos "eus" passados e futuros

5. Na quarta dimensão, a cada momento, uma série de variáveis define o que seremos no instante seguinte. A versão que fica (o eu "normal") é apenas uma entre infinitas que poderiam rolar (como o "eu viking", "eu pirata" e "eu palhaço"). A quinta dimensão é o conjunto de todas essas versões

6. A sexta dimensão é o caminho entre as possibilidades da 5D. Seria como se todas as suas infinitas versões estivessem dispostas em um plano, como uma folha, e você pudesse dobrar essa folha, encostando um lado (o "eu normal", por exemplo) em outro lado (como o "eu viking")

7a. Os vários "eus" possíveis da 6D estão dentro de um universo. A sétima dimensão pega o conceito de linha temporal da 4D e aplica a todo esse universo, traçando uma linha do tempo que começa no big-bang, evento que teria dado início a tudo

7b. Mas não é só: a sétima dimensão também diz que, assim como cada um de nós, o universo também pode ter várias versões, e estabelece que existem universos alternativos ao nosso, originados do mesmo big-bang


7c. O "nosso" big-bang é apenas uma possibilidade. Podem existir outros big-bangs diferentes que podem ter dado origem a outros universos, os quais também podem ter infinitas versões. A 7D reúne todos os big-bangs e todos os infinitos universos possíveis

8. Imagine que cada uma dessas bolinhas da imagem acima é um dos big-bangs (com seus respectivos universos derivados) existentes na sétima dimensão. A oitava dimensão é um vértice, um ponto de intersecção a partir do qual se pode chegar a qualquer uma das "bolinhas"

9. Partindo da figura da 8D, imagine que o vértice é um ponto onde o plano formado antes pode ser dobrado. A nona dimensão nada mais é do que uma dobra nesse plano, para encostar um big-bang no outro e permitir viajar entre eles - como as viagens entre os "eus" na 6D

10. A décima dimensão é o conjunto de todos os caminhos para todos os big-bangs, que dão origem a todos os universos. Imagine pegar todas as nove dimensões e juntar tudo num pontinho. Essa é a décima dimensão - o fim do caminho, de onde não há mais para onde ir

Como desmontar frações

Quando a Matemática era ensinada com prazer e os bons professores estimulavam os alunos com descobertas lúdicas, "contar ladrilhos" ajudava a entender operações com frações. Veja como a tabuada de multiplicar fica mais fácil.

Por Luiz Barco

1. Associar a multiplicação às áreas de um retângulo permite uma consistente aplicação da Aritmética. Três colunas de dois ladrilhos, como mostra o conjunto destacado ao lado, são seis ladrilhos, ou seja 2 x 3 = 6.

2. Só que outro dia uma professora primária me pediu um jeito de explicar porque, para se multiplicar frações, faz-se diretamente a multiplicação dos numeradores e denominadores, enquanto a adição tem todo aquela complicação de achar o mínimo múltiplo comum. Achei que uma boa justificativa geométrica, aplicada às frações, resolveria. A explicação é muito interessante. Preste atenção.

3. Pegue um quadrado unitário e marque nele a fração 2/3 (isto é, divida-o em 3 partes equivalentes e tome 2 dessas partes). O retângulo pintado representa 2/3 da unidade. Repare que ele tem comprimento igual a 1 e largura de 2/3 da unidade.

4. Faça o mesmo com a fração 4/7 da unidade.

5. Sem pintura, mas mantendo as divisões, faça a fusão das duas imagens deslizando um quadrado sobre o outro. A seguir, marque os 2/3 com bolinhas e os 4/7 com um pequeno x.

6. Repare que fica marcado, pela bolinha e pelo x, o retângulo cujo comprimento é 4/7 da unidade e cuja largura é 2/3 da unidade. É razoável pensar que a área seja 2/3 x 4/7.

7. Ora! Se voltarmos ao quadrado grande, vamos verificar que ele foi dividido em 21 partes (3 linhas com 7 colunas cada uma). É portanto correto pensarmos em 1/21 (cada pedacinho). Desses, temos somente 8 (2 linhas com 4 colunas) com as duas marquinhas, isto é: o retângulo em destaque, 2/3 x 4/7, é de fato 8/21 do quadrado unitário. Assim, fica fácil definir:

Luiz Barco, professor da Universidade de São Paulo (USP) e da Universidade Estadual de Campinas (Unicamp) matematica@abril.com.br

Algumas das mais antigas frações conhecidas estâo no Papiro Rhind, feito no Egito, no século XVII a.C., hoje no Museu Britânico, em Londres. Ele contém uma tábua de frações destinadas a resolver operaçôes de divisão mais a solução de 84 problemas de Aritmética e Geometria.

A jovem professora tem aí uma maneira de justificar aos seus alunos a multiplicação de frações. É claro que isso é apenas uma justificativa e não uma prova com o rigor que satisfaça a um purista, mas que a criançada entende, ah!, isso entende. Os livros didáticos mostram, quando ocorre essa operação matemática, uma justificativa algébrica (na minha opinião, bem mais abstrata), mas creio que o professor deve valer-se também dela. Acredito que o ver (não apenas com os olhos) antecede o abstrair. Ambos são importantes. Por isso, espero que o exemplo acima seja exaustivamente explorado pela professora e seus alunos até que todos considerem natural misturar a multiplicação com a área de um retângulo.

Agora é com você. Ache uma maneira geométrica de justificar a adição 2/3 + 4/7. Brinque com as figuras e com o que elas significam (em frações). Mesmo que não consiga chegar a uma solução, você passará algum tempo sem pensar em impostos, governantes e sindicatos e deixará a mente fluir. Perçeba que o mundo é mais simples do que em geral se pensa e que as pessoas são mais complicadas do que talvez devessem.

 

Fractais, ciência e artes misturadas 

 

A ciência dos fractais apresenta estruturas geométricas de grande complexidade e beleza infinita, ligadas às formas da natureza, ao desenvolvimento da vida e à própria compreensão do universo. São imagens de objetos abstratos que possuem o caráter de onipresença por terem as características do todo infinitamente multiplicadas dentro de cada parte, escapando assim, da compreensão em sua totalidade pela mente humana.      Essa geometria, nada convencional, tem raízes remontando ao século XIX e algumas indicações neste sentido vêm de muito antes, na Grécia Homérica, Índia, China, entre outros. Porém, somente há poucos anos vem se consolidando com o desenvolvimento dos computadores e o auxílio de novas teorias nas áreas da física, biologia, astronomia, matemática e outras. Os fractais foram nomeados - ao invés de descobretos ou inventados - no início dos anos 80 por Benoît Mandelbrot, o "pai dos fractais", para classificar certos objetos intrincados que não possuem dimensão inteira (1, 2 ou 3) mas sim fracionária (dimensão 1,85 por exemplo).
     Diferentes definições de Fractais surgiram com o aprimoramento de sua teoria. A noção que serve de fio condutor foi introduzida por Benoît Mandelbrot através do neologismo "Fractal", que surgiu do adjetivo latino fractus, que significa "irregular" ou "quebrado".
      Uma primeira definição, pelo próprio Mandelbrot, diz: - "Um conjunto é dito Fractal se a dimensão Hausdorff-Besicovitch deste conjunto for maior do que sua dimensão topológica". No decorrer do tempo ficou claro que esta definição era muito restritiva embora tenha motivações pertinentes.
     Os fractais podem apresentar uma infinidade de formas diferentes, não existindo uma aparência consensual. Contudo, existem duas características muito freqüentes nesta geometria: auto-semelhança e complexidade infinita.
     Distante do rigor e do formalismo matemático, pode-se definir Fractais, como nos ensinam alguns estudiosos da área: "Objetos que apresentam auto-semelhança e complexidade infinita, ou seja, têm sempre cópias aproximadas de sí mesmo em seu interior."
      A Geometria Fractal pode ser utilizada para descrever diversos fenômenos na natureza, onde não pode ser utilizada as geometrias tradicionais. "Núvens não são esferas, montanhas não são cones, continentes não são círculos, um latido não é contínuo e nem o raio viaja em linha reta." - Benoit Mandelbrot 

 Padrões para preenchimento de PENROSE

CURIOSADES MATEMÁTICAS

SABE O QUE É NÚMERO MÁGICO?

1089 é conhecido como o número mágico. Veja porque:

Escolha qualquer número de três algarismos distintos: por exemplo, 875.
Agora escreva este número de trás para frente e subtraia o menor do maior:
875 - 578 = 297

Agora inverta também esse resultado e faça a soma:
297 + 792 = 1089  (o número mágico)

 Curiosidade com números de três algarismos

Escolha um numero de três algarismos:
Ex: 234
Repita este numero na frente do mesmo:
234234
Agora divida por 13:
234234 / 13 = 18018
Agora divida o resultado por 11:
18018 / 11 = 1638
Divida novamente o resultado, só que agora por 7:
1638 / 7 = 234
O resultado é igual ao numero de três algarismos que você havia escolhido: 234.

CURIOSIDADE SOBRE NÚMEROS QUADRADOS PERFEITOS

 Os pares de quadrados perfeitos:

144 e 441, 169 e 961, 14884 e 48841

e suas respectivas raízes:

12 e 21, 13 e 31, 122 e 221, são formados pelos mesmos algarismos, porém escritos em ordem inversa.

O matemático Thébault investigou os pares que têm esta curiosa propiedade. Encontrou, por exemplo, a seguinte dupla:

1113² = 1.238.769   e   3111² = 9.678.321

O NÚMERO PI  

Na matemática, é uma proporção numérica originada da relação entre as grandezas do perímetro de uma circunferência e seu diâmetro; por outras palavras, se uma circunferência tem perímetro e diâmetro , então aquele número é igual a 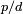. É representado pela letra grega π. A letra grega π (lê-se: pi), foi adotada para o número a partir da palavra grega para perímetro, "περίμετρος", provavelmente por William Jones em 1706, e popularizada por Leonhard Euler alguns anos mais tarde. Outros nomes para esta constante são constante circular, constante de Arquimedes ou número de Ludolph.

O valor de π pertence aos números irracionais. Para a maioria dos cálculos simples é comum aproximar com 31 casas decimais. Para cálculos ainda mais precisos pode-se obter aproximações de π através de algoritmos computacionais. por 3,14. Uma boa parte das calculadoras científicas de 8 dígitos aproxima por 3,1415927. Para cálculos mais precisos pode-se utiliza.

Desde a Antiguidade, foram encontradas várias aproximações de π para o cálculo da área do círculo. Entre os egípcios, por exemplo no papiro de Ahmes, o valor atribuído a π seria , embora também seja encontrado o valor . Na Bíblia (1 Reis 7:23) é possível encontrar que os hebreus utilizavam o valor 3 como aproximação de π . 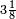Entre os babilônios, era comum o uso do valor 3 para calcular a área do círculo, apesar de o valor já ser conhecido como aproximação.

Formulação matemática do método de Arquimedes

Baseado no método de Arquimedes é possível formular uma representação matemática para o cálculo de pi, eficiente para um polígono de qualquer número de lados.

Considerando um polígono de n lados e raio 1, temos a medida do lado expressa pela lei dos cossenos:

a² = b² + c² − 2abcosα

Temos formado um triângulo isósceles, de base l e lados r=1:

l² = r² + r² − 2r²cosα
l² = 1² + 1² − 2cosα
l² = 2 − 2cosα

O ângulo do triângulo isósceles no centro do polígono é expresso por 360º dividido pelo número de lados (n), portanto:

Dessa forma, o perímetro do polígono será de:

Como π é representado pelo perímetro do polígono dividido pelo seu diâmetro, temos:

Grandezas que dependem de π

Várias relações matemáticas dependem do conhecimento da constante π, as mais conhecidas a nível didático são:

• Perímetro de uma circunferência:
• Área do círculo :
• Volume de uma esfera:

π também está nas fórmulas gravitacionais e do eletromagnetismo da física.

 

AULÃO META PARA O ENEM !!!

GALERA ESTAREMOS REALIZANDO NO PRÓXIMO DIA 30 DE OUTUBRO O NOSSO AULÃO PARA O ENEM 2010! CONFIRAM OS DETALHES E VAMOS COMPARECER ....

ESTAREI JUNTO COM O PROFESSOR MARCELO E PROFESSOR FELÍCIO DANDO DICAS PARA O NOVO ENEM...COMO VCS SABEM MATEMÁTICA E SUAS TECNOLOGIAS DEVEM SER ENCARADAS COM MUITA CONTEXTUALIZAÇÃO E BASTANTE ATENÇÃO NAS COMPETÊNCIAS QUE DIZEM RESPEITO A LEITURA DE GRÁFICOS, TABELAS, INTERPRETAÇÕES DE PORCENTAGEM, E INTERPRETAÇÕES GEOMÉTRICAS.

NOSSA EQUIPE DO META ESTÁ ANTENADA COM AS NOVIDADES PARA ESSE ENEM, CONFIRAM EM NOSSO SITE AS NOVIDADES E ACOMPANHEM PELO MEU BLOG ALGUMAS NOVIDADES...ABRAÇO A TODOS OS MEUS QUERIDOS ALUNOS E TORÇO POR VCS POIS MERECEMOS ESSA VITÓRIA NOS VESTIBULARES E ENEM

DAQUI A POUCO PONHO UMA LISTA DE SITES PARA TURBINAR O ESTUDO DE VCS!!!