Escolha qualquer número de três algarismos distintos: por exemplo, 875.
Agora escreva este número de trás para frente e subtraia o menor do maior:
875 - 578 = 297
Agora escreva este número de trás para frente e subtraia o menor do maior:
875 - 578 = 297
Agora inverta também esse resultado e faça a soma:
297 + 792 = 1089 (o número mágico)
297 + 792 = 1089 (o número mágico)
Escolha um numero de três algarismos:
Ex: 234
Repita este numero na frente do mesmo:
234234
Agora divida por 13:
234234 / 13 = 18018
Agora divida o resultado por 11:
18018 / 11 = 1638
Divida novamente o resultado, só que agora por 7:
1638 / 7 = 234
O resultado é igual ao numero de três algarismos que você havia escolhido: 234.
Ex: 234
Repita este numero na frente do mesmo:
234234
Agora divida por 13:
234234 / 13 = 18018
Agora divida o resultado por 11:
18018 / 11 = 1638
Divida novamente o resultado, só que agora por 7:
1638 / 7 = 234
O resultado é igual ao numero de três algarismos que você havia escolhido: 234.
CURIOSIDADE SOBRE NÚMEROS QUADRADOS PERFEITOS
Os pares de quadrados perfeitos:
144 e 441, 169 e 961, 14884 e 48841
e suas respectivas raízes:
12 e 21, 13 e 31, 122 e 221, são formados pelos mesmos algarismos, porém escritos em ordem inversa.
O matemático Thébault investigou os pares que têm esta curiosa propiedade. Encontrou, por exemplo, a seguinte dupla:
11132 = 1.238.769 e 31112 = 9.678.321
O NÚMERO PI
Na matemática,  é uma proporção numérica originada da relação entre as grandezas do perímetro de uma circunferência e seu diâmetro; por outras palavras, se uma circunferência tem perímetro
é uma proporção numérica originada da relação entre as grandezas do perímetro de uma circunferência e seu diâmetro; por outras palavras, se uma circunferência tem perímetro  e diâmetro
e diâmetro  , então aquele número é igual a
, então aquele número é igual a 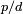 . É representado pela letra grega π. A letra grega π (lê-se: pi), foi adotada para o número a partir da palavra grega para perímetro, "περίμετρος", provavelmente por William Jones em 1706, e popularizada por Leonhard Euler alguns anos mais tarde. Outros nomes para esta constante são constante circular, constante de Arquimedes ou número de Ludolph.
. É representado pela letra grega π. A letra grega π (lê-se: pi), foi adotada para o número a partir da palavra grega para perímetro, "περίμετρος", provavelmente por William Jones em 1706, e popularizada por Leonhard Euler alguns anos mais tarde. Outros nomes para esta constante são constante circular, constante de Arquimedes ou número de Ludolph.
 é uma proporção numérica originada da relação entre as grandezas do perímetro de uma circunferência e seu diâmetro; por outras palavras, se uma circunferência tem perímetro
é uma proporção numérica originada da relação entre as grandezas do perímetro de uma circunferência e seu diâmetro; por outras palavras, se uma circunferência tem perímetro  e diâmetro
e diâmetro  , então aquele número é igual a
, então aquele número é igual a 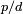 . É representado pela letra grega π. A letra grega π (lê-se: pi), foi adotada para o número a partir da palavra grega para perímetro, "περίμετρος", provavelmente por William Jones em 1706, e popularizada por Leonhard Euler alguns anos mais tarde. Outros nomes para esta constante são constante circular, constante de Arquimedes ou número de Ludolph.
. É representado pela letra grega π. A letra grega π (lê-se: pi), foi adotada para o número a partir da palavra grega para perímetro, "περίμετρος", provavelmente por William Jones em 1706, e popularizada por Leonhard Euler alguns anos mais tarde. Outros nomes para esta constante são constante circular, constante de Arquimedes ou número de Ludolph.O valor de π pertence aos números irracionais. Para a maioria dos cálculos simples é comum aproximar  com 31 casas decimais. Para cálculos ainda mais precisos pode-se obter aproximações de π através de algoritmos computacionais. por 3,14. Uma boa parte das calculadoras científicas de 8 dígitos aproxima por 3,1415927. Para cálculos mais precisos pode-se utiliza.
com 31 casas decimais. Para cálculos ainda mais precisos pode-se obter aproximações de π através de algoritmos computacionais. por 3,14. Uma boa parte das calculadoras científicas de 8 dígitos aproxima por 3,1415927. Para cálculos mais precisos pode-se utiliza.
 com 31 casas decimais. Para cálculos ainda mais precisos pode-se obter aproximações de π através de algoritmos computacionais. por 3,14. Uma boa parte das calculadoras científicas de 8 dígitos aproxima por 3,1415927. Para cálculos mais precisos pode-se utiliza.
com 31 casas decimais. Para cálculos ainda mais precisos pode-se obter aproximações de π através de algoritmos computacionais. por 3,14. Uma boa parte das calculadoras científicas de 8 dígitos aproxima por 3,1415927. Para cálculos mais precisos pode-se utiliza.Desde a Antiguidade, foram encontradas várias aproximações de π para o cálculo da área do círculo. Entre os egípcios, por exemplo no papiro de Ahmes, o valor atribuído a π seria  , embora também seja encontrado o valor
, embora também seja encontrado o valor  . Na Bíblia (1 Reis 7:23) é possível encontrar que os hebreus utilizavam o valor 3 como aproximação de π . Entre os babilônios, era comum o uso do valor 3 para calcular a área do círculo, apesar de o valor
. Na Bíblia (1 Reis 7:23) é possível encontrar que os hebreus utilizavam o valor 3 como aproximação de π . Entre os babilônios, era comum o uso do valor 3 para calcular a área do círculo, apesar de o valor 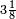 já ser conhecido como aproximação.
já ser conhecido como aproximação.
 , embora também seja encontrado o valor
, embora também seja encontrado o valor  . Na Bíblia (1 Reis 7:23) é possível encontrar que os hebreus utilizavam o valor 3 como aproximação de π . Entre os babilônios, era comum o uso do valor 3 para calcular a área do círculo, apesar de o valor
. Na Bíblia (1 Reis 7:23) é possível encontrar que os hebreus utilizavam o valor 3 como aproximação de π . Entre os babilônios, era comum o uso do valor 3 para calcular a área do círculo, apesar de o valor 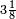 já ser conhecido como aproximação.
já ser conhecido como aproximação.Formulação matemática do método de Arquimedes
Baseado no método de Arquimedes é possível formular uma representação matemática para o cálculo de pi, eficiente para um polígono de qualquer número de lados.
Considerando um polígono de n lados e raio 1, temos a medida do lado expressa pela lei dos cossenos:
a2 = b2 + c2 − 2abcosα
Temos formado um triângulo isósceles, de base l e lados r=1:
l2 = r2 + r2 − 2r2cosα
l2 = 12 + 12 − 2cosα
l2 = 2 − 2cosα

l2 = 12 + 12 − 2cosα
l2 = 2 − 2cosα

O ângulo do triângulo isósceles no centro do polígono é expresso por 360º dividido pelo número de lados (n), portanto:

Dessa forma, o perímetro do polígono será de:

Como π é representado pelo perímetro do polígono dividido pelo seu diâmetro, temos:

Grandezas que dependem de π
Várias relações matemáticas dependem do conhecimento da constante π, as mais conhecidas a nível didático são:
- Perímetro de uma circunferência:
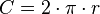
- Área do círculo :
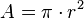
- Volume de uma esfera:




Nenhum comentário:
Postar um comentário